วงล้อหรรษาพากันเล่น

เวลาที่ใช้ 1 คาบ

ชื่อกิจกรรม วงล้อหรรษาพากันเล่น

วัตถุประสงค์ของกกิจกรรม

         เพื่อให้นักเรียนเขียนความน่าจะเป็นของเหตุการณ์ที่กำหนดให้ได้

กลุ่มเป้าหมาย

นักเรียนระดับชั้นมัธยมศึกษาตอนต้น

อุปกรณ์

วงล้อหรรษาจำนวน 4 รูปแบบ

ขั้นตอนการทำกิจกรรม

ขั้นนำ

          1. ครูหยิบวงล้อทั้ง 4 แบบ ออกมาให้นักเรียนดู นักเรียนตอบคำถาม ดังนี้

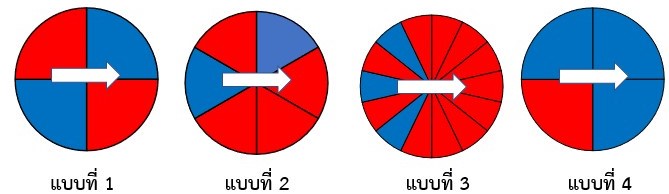
                   - นักเรียนทายว่าสีใดในวงล้อแบบที่ 1 จะมีโอกาสออกบ่อยที่สุด (นักเรียนอาจตอบว่าสีแดงหรือสีน้ำเงินก็ได้)

                   - นักเรียนทายว่าสีใดในวงล้อแบบที่ 2 จะมีโอกาสออกบ่อยที่สุด (นักเรียนอาจตอบว่าสีแดงหรือสีน้ำเงินก็ได้)

                   - นักเรียนทายว่าสีใดในวงล้อแบบที่ 3 จะมีโอกาสออกบ่อยที่สุด (นักเรียนอาจตอบว่าสีแดงหรือสีน้ำเงินก็ได้)

                   - นักเรียนทายว่าสีใดในวงล้อแบบที่ 4 จะมีโอกาสออกบ่อยที่สุด (นักเรียนอาจตอบว่าสีแดงหรือสีฟ้าก็ได้)

ขั้นสอน

         2. ครูชี้แจงกติกาการเล่น ให้นักเรียนแต่ละกลุ่มทดลองหมุนวงล้อที่ได้รับ จำนวน 20 ครั้ง พร้อมทั้งบันทึกผลลงสมุด โดยให้นักเรียนออกแบบตารางการบันทึกผลเอง ภายในเวลา 15 นาที

         3. ครูให้นักเรียนแบ่งกลุ่มจำนวน 5 กลุ่ม

         4. นักเรียนแต่ละกลุ่มได้รับวงล้อ 4 รูปแบบที่แตกต่างกัน เพื่อนำไปทดลองหมุนวงล้อหรรษาพากันเล่น

         5. เมื่อนักเรียนทดลองครบทุกกลุ่มแล้ว ครูให้นักเรียนแต่ละกลุ่มส่งตัวแทน 1 คน มานำเสนอผลจากการหมุนวงล้อของกลุ่มตนเอง ว่าสีแดงออกจำนวนกี่ครั้ง สีน้ำเงินออกจำนวนกี่ครั้ง ภายในเวลา 1 นาที (นักเรียนตอบได้ตามอิสระโดยอาศัยข้อมูลจากตารางการบันทึกผล)

         6. นักเรียนตอบคำถามจากการทดลองหมุนวงล้อหรรษา ดังนี้

                   - ถ้านักเรียนทำการทดลองหมุนวงล้อวงล้อแบบที่ 1 จำนวน 1 ครั้ง ผลลัพธ์ที่จะเกิดขึ้นมีทั้งหมดกี่เหตุการณ์ (4 เหตุการณ์)

                   - ถ้าครูสนใจเพียงเหตุการณ์ที่หมุนวงล้อไปหยุดที่สีแดงมีกี่เหตุการณ์ (2 เหตุการณ์)          

                   - นักเรียนเขียนอัตราส่วนของเหตุการณ์ที่หมุนวงล้อไปหยุดที่สีแดงต่อเหตุการณ์ทั้งหมดที่เกิดขึ้นได้อย่างไร (2/4 หรือ 1/2)

                   - เรียกอัตราส่วนของเหตุการณ์ที่หมุนวงล้อไปหยุดที่สีแดงต่อเหตุการณ์ทั้งหมดที่เกิดขึ้นได้ทั้งหมดนี้ว่าอย่างไร (ความน่าจะเป็นของเหตุการณ์)

7. ครูอธิบายเชื่อมโยงสู่สูตรความน่าจะเป็น ดังนี้

ความน่าจะเป็นของเหตุการณ์ใด เท่ากับ อัตราส่วนของจำนวนผลที่จะเกิดเหตุการณ์นั้นต่อจำนวนผลทั้งหมดที่อาจเกิดขึ้นได้

            หรือ ความน่าจะเป็นของเหตุการณ์ใด =

เมื่อผลทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่ม แต่ละตัวมีโอกาสเกิดขึ้นได้เท่าๆ กัน

กำหนดให้       E       เป็นเหตุการณ์ที่เราสนใจ

                   P(E)    เป็นความน่าจะเป็นของเหตุการณ์ E

                   N       เป็นจำนวนสมาชิกทั้งหมดที่เกิดขึ้นได้จากการทดลองสุ่ม

และ              n       เป็นจำนวนสมาชิกของเหตุการณ์ที่เราสนใจ

                   ดังนั้น                       P(E) =      

8. ให้นักเรียนแต่ละกลุ่มหาความน่าจะเป็นของสีแดง และ ความน่าจะเป็นของสีน้ำเงิน ในวงล้อหรรษาที่แต่ละกลุ่มที่ได้รับ จากนั้นให้นักเรียนแต่ละกลุ่มส่งตัวแทน 1 คนมานำเสนอ โดยมีคำถามดังนี้

                   - สีใดในวงล้อแบบที่ 1 จะมีโอกาสออกบ่อยที่สุด เพราะเหตุใด (มีโอกาสเท่ากัน เพราะ ความน่าจะเป็นที่จะออกสีแดง เท่ากับ หรือ หรือ 0.5 และความน่าจะเป็นที่จะออกสีน้ำเงิน เท่ากับ หรือ หรือ 0.5 ซึ่งทั้งสองสีมีความน่าจะเป็นของเหตุการณ์ที่เท่ากัน)

                   - สีใดในวงล้อแบบที่ 2 จะมีโอกาสออกบ่อยที่สุด เพราะเหตุใด (สีแดง เพราะ ความน่าจะเป็นที่จะออกสีแดง เท่ากับ หรือ หรือ และความน่าจะเป็นที่จะออกสีน้ำเงิน เท่ากับ หรือ หรือ ซึ่งความน่าจะเป็นของสีแดงมากกว่าความน่าจะเป็นของสีน้ำเงิน)

                   - สีใดในวงล้อแบบที่ 3 จะมีโอกาสออกบ่อยที่สุด เพราะเหตุใด (สีแดง เพราะ ความน่าจะเป็นที่จะออกสีแดง เท่ากับ หรือ และความน่าจะเป็นที่จะออกสีน้ำเงิน เท่ากับ หรือ ซึ่งความน่าจะเป็นของสีแดงมากกว่าความน่าจะเป็นของสีน้ำเงิน)

                   - สีใดในวงล้อแบบที่ 4 จะมีโอกาสออกบ่อยที่สุด เพราะเหตุใด (สีน้ำเงิน เพราะ ความน่าจะเป็นที่จะออกสีแดง เท่ากับ หรือ และความน่าจะเป็นที่จะออกสีน้ำเงิน เท่ากับ หรือ ซึ่งความน่าจะเป็นของสีน้ำเงินมากกว่าความน่าจะเป็นของสีแดง) 

ขั้นสรุป

         9. ครูและนักเรียนร่วมกันอภิปรายและสรุปเกี่ยวกับความน่าจะเป็นของเหตุการณ์ร่วมกัน ดังนี้

ความน่าจะเป็นที่เท่ากับ 0 ก็คือไม่มีโอกาสที่เหตุการณ์นั้นจะเกิดขึ้น แต่ถ้าความน่าจะเป็นเท่ากับ 1 แสดงว่าเหตุการณ์เหล่านั้นเกิดขึ้นได้อย่างแน่นอน นั่นหมายความว่ายิ่งความน่าจะเป็นเข้าใกล้ 1 ความเป็นไปได้ที่จะเกิดเหตุการณ์นั้นยิ่งสูงขึ้น

ข้อมูลอ้างอิง

หนังสือ Elementary and Middle School Mathematics Teaching Developmentally ของ John A. Van de Walle, Karen S. Karp and Jennifer M. Bay-Williams

อาจารย์ที่ปรึกษา อาจารย์ ดร.รัชนิกร ชลไชยะ คณะวิทยาศาสตร์ ภาควิชาคณิตศาสตร์ มหาวิทยาลัยเทคโนโลยีพระจอมเกล้าธนบุรี

หนังสือเรียนสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี (สสวท.) กระทรวงศึกษาธิการ