คุณครูคณิตศาสตร์ไม่มากก็น้อย ต้องเคยได้ยินเรื่องราวเกี่ยวกับคำถามของนักเรียนที่ว่าทำไมการคูณจำนวนถึงมีสมบัติการสลับที่ แต่ในฐานะครูคณิตศาสตร์เราจะตอบและอธิบายให้นักเรียนเข้าใจได้อย่างไร และสิ่งที่เราจะอธิบายนั้นเชื่อมโยงกับความรู้เดิมของนักเรียนได้มากน้อยเพียงใด เพื่อการอธิบายสมบัติการสลับที่การคูณ ผู้เขียนได้ใช้แนวคิดของพื้นที่ของรูปสี่เหลี่ยมมุมฉาก ซึ่งเกิดจากความยาวคูณด้วยความกว้างโดยแสดงในรูปของ Array Model เช่น แสดงแทน 5 x 6 ด้วยพื้นที่ของรูปสี่เหลี่ยมมุมฉากกว้าง 5 หน่วย ยาว 6 หน่วย ดังภาพที่ 1

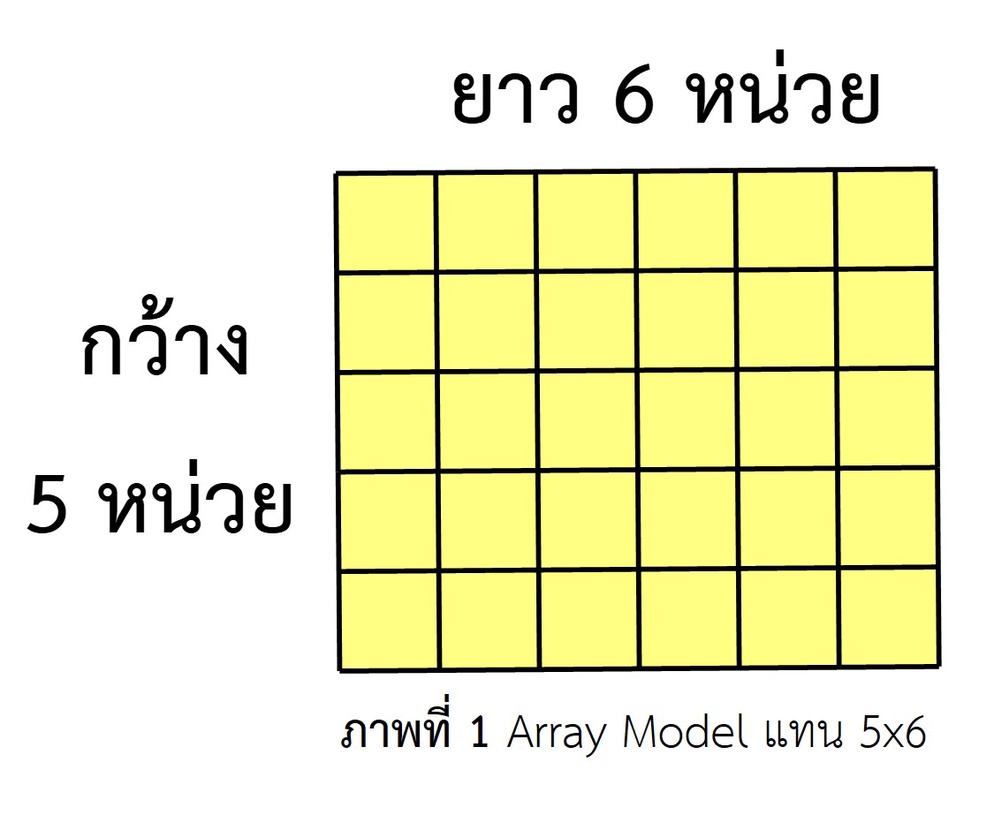
แน่นอนว่าผลลัพธ์ของ 5 x 6 สามารถหาได้จากการนับจำนวนช่องทั้งหมดที่ปรากฏ นั่นคือ 30 นั่นคือ พื้นที่ของรูปสี่เหลี่ยมมุมฉากขนาดกว้าง 5 หน่วย ยาว 6 หน่วย เท่ากับ 30 ตารางหน่วยด้วย เมื่อนักเรียนเข้าใจส่วนนี้ดีแล้ว การสอนสมบัติสลับที่การคูณก็ไม่ยากอีกต่อไป เริ่มจากให้ทางซ้ายมือเป็นตัวตั้งและทางด้านบนเป็นตัวคูณ ดังภาพที่ 2

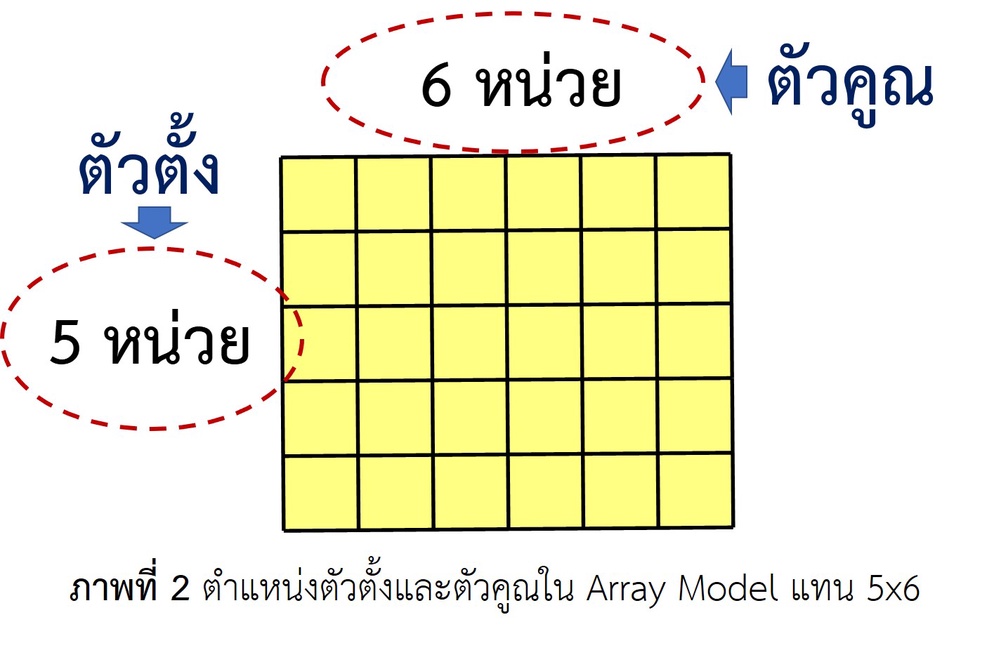
จากภาพที่ 2 นักเรียนจะเข้าใจว่า 5 x 6 = 30 จากนั้น ทำการหมุน Array ไปทางซ้าย 90 องศา จะทำให้ตัวตั้งกลายเป็น 6 หน่วย และตัวคูณเป็น 5 หน่วย ซึ่งแสดงได้ด้วย 6 x 5 และยังมีค่าเท่าเดิม คือ 30 เพราะว่ายังเป็นพื้นที่ขนาดเท่าเดิมไม่เปลี่ยนแปลง แสดงดังภาพที่ 3

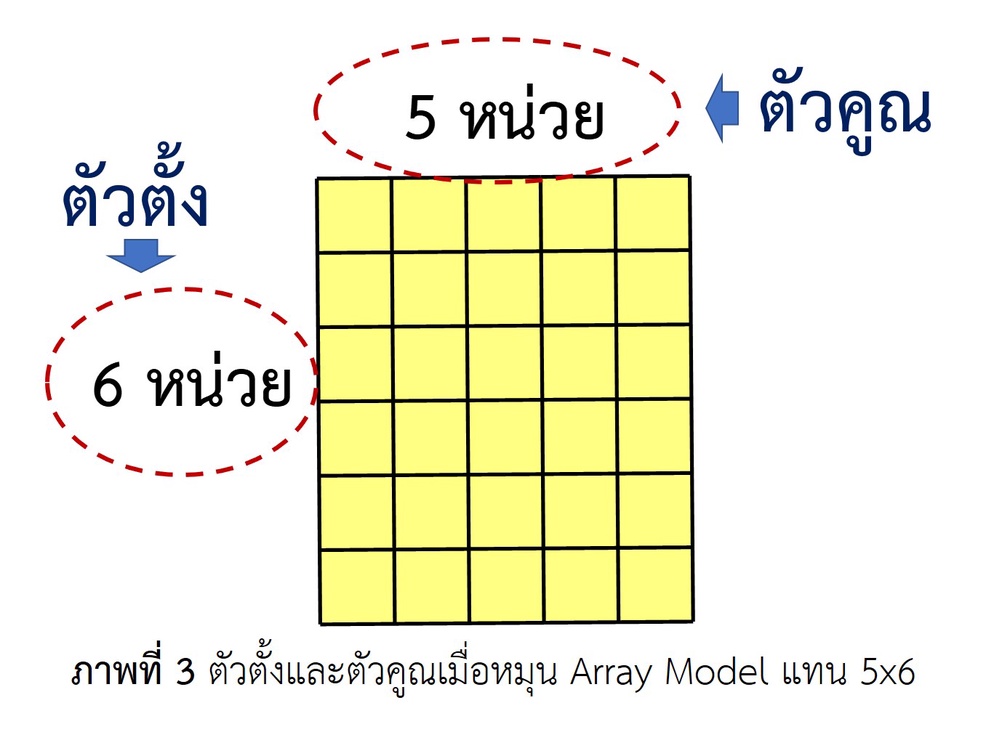
ท้ายที่สุดนักเรียนจะเห็นว่า 5x6 = 6x5 นั่นคือ การคูณมีสมบัติสลับที่ นั่นเอง

สำหรับการสร้างสื่อเพื่อประกอบการอธิบาย ผู้เขียนได้ใช้โปรแกรม GSP เพื่อทำให้ Array Model สามารถเคลื่อนไหวบนระนาบและปรับขนาดได้ (Supplementary File) เมื่อนำไปใช้ประกอบการอธิบายนักเรียนจะเห็นและรับรู้ได้ถึงการหมุนที่ชัดเจนยิ่งขึ้น และจดจำภาพไปใช้จินตนาการถึงการคูณของจำนวนเต็มในรูป Array Model ในใจได้ ดังภาพที่ 4

แนวคิดนี้สังเคราะห์และพัฒนามาจากหลักการจัดการเรียนรู้ของ Bruner ที่อธิบายว่า การเรียนการสอนสามารถใช้รูปแบบแสดงแทนทางความคิดเพื่อช่วยให้นักเรียนเกิดความเข้าใจได้ 3 รูปแบบ ได้แก่ การแสดงแทนความคิดด้วยการกระทำ (Enactive Representation) การแสดงแทนความคิดด้วยการนึกภาพ (Iconic Representation) และการแสดงแทนความคิดด้วยสัญลักษณ์ (Symbolic Representation) ในสื่อนี้ใช้การแสดงแทนความคิดด้วยการนึกภาพ และไปสู่การแสดงแทนความคิดด้วยสัญลักษณ์ และการตัวแสดงแทนเชิงคณิตศาสตร์ (Mathematical Representation) ที่เหมาะสมเพื่อสร้างความเข้าใจให้กับนักเรียนดังที่ NCTM (2014) อธิบายว่า นักเรียนจะมีความเข้าใจมากขึ้นหากได้เรียนรู้และทำความเข้าใจผ่านตัวแสดงแทนเชิงคณิตศาสตร์มากกว่า 1 ชนิด สำหรับการสอนเรื่องสมบัติการแจกแจงของจำนวนก็สามารถใช้แนวคิดของ Array Model ได้เช่นกัน (โปรดติดตามต่อไป)